How Does It Work? Core Cryptographic Techniques Explained, Simply

This blog explains how encryption, hashes, digital signatures and zero-knowledge proofs secure data and enable trust in digital systems.

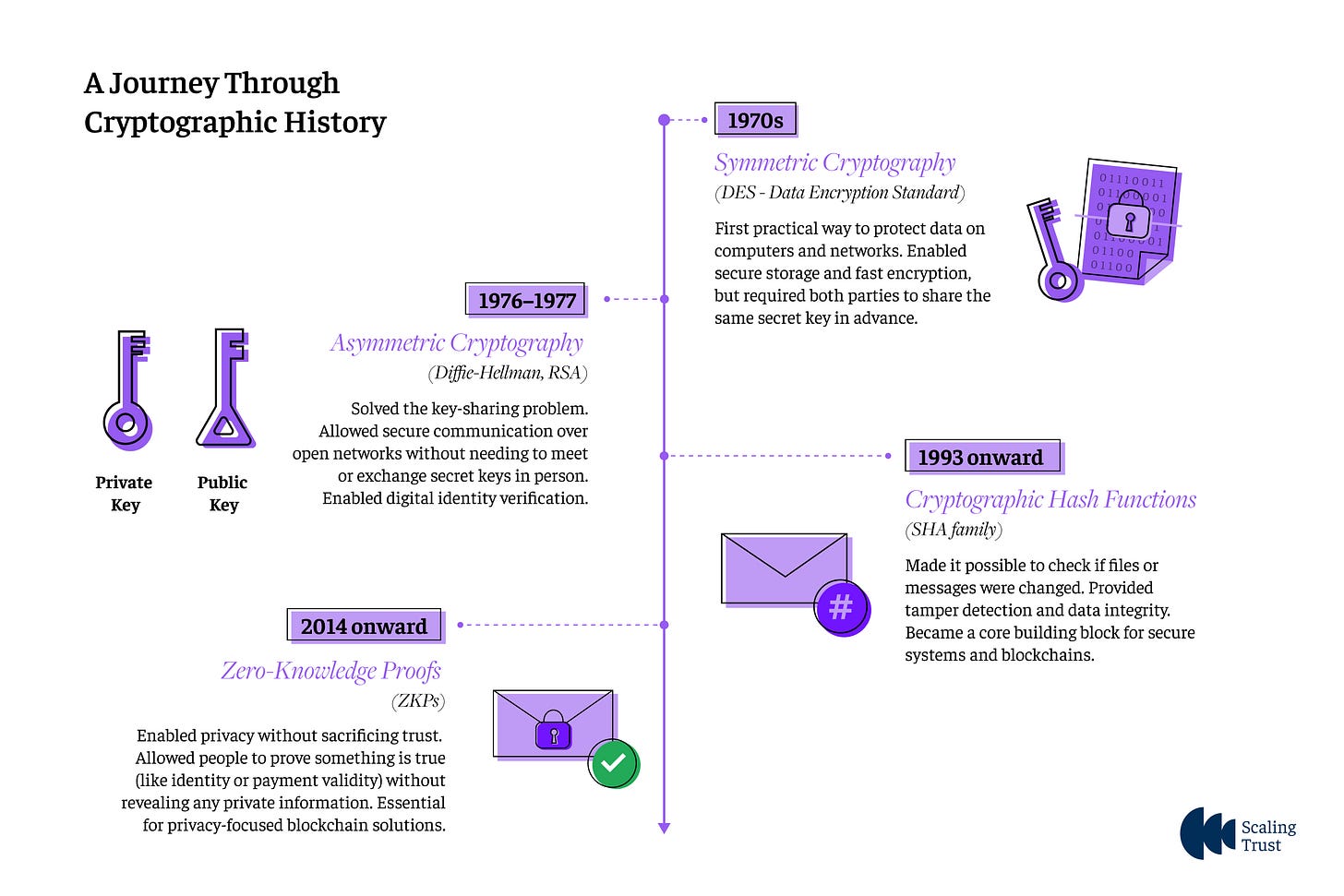
In Part 1 of this series, we explored how cryptography evolved from ancient ciphers to the modern systems that secure our digital world and how it has become the foundation for digital trust. Now, in Part 2, we move beyond history to understand how cryptography actually works under the hood. To quickly recap, cryptography is the science of protecting information by transforming it into a secure format that can only be understood by the intended parties. It enables privacy, authentication, and secure communication, making it a cornerstone of the digital world. You can revisit our earlier blog for a deeper dive into how cryptography has shaped the evolution of digital trust.

In this part, we break down four core building blocks of modern cryptography: symmetric and asymmetric encryption, hash functions, digital signatures, and zero-knowledge proofs. Understanding these fundamentals provides insight into how digital security, privacy, and decentralized systems like blockchain are made possible. We will keep the concepts accessible, using relatable, real-world examples to explain why these tools are critical for securing information and building trust online.

Symmetric vs. Asymmetric Encryption

To understand how encryption works in the real world, let’s take the example of two friends, Sandhya and Azam, who often exchange important information online. But, like all of us, they want to make sure that their messages stay private and cannot be intercepted or read by anyone else.

Symmetric Encryption: Sharing a Secret Key

Imagine Sandhya and Azam both have identical keys to the same locked box. Whenever Sandhya wants to send a message to Azam, she writes it down, locks it in the box using their shared key, and sends the box to him. Azam uses his copy of the same key to unlock the box and read the message. This is how symmetric encryption works. A single secret key is used for both encrypting and decrypting the data. This method is simple and extremely fast, making it ideal for protecting large amounts of information. For example, symmetric encryption algorithms like AES (Advanced Encryption Standard) are widely used to secure data stored on hard drives, files, databases, and for fast, secure communications such as VPN connections (Daemen & Rijmen, 2002).

But there is a challenge. How did Sandhya and Azam both get copies of the same key in the first place? In real-world networks, securely sharing that secret key can be difficult. If someone intercepts the key during the exchange, the entire system is compromised. This key distribution problem is one of the main limitations of symmetric encryption.

Asymmetric Encryption: Solving the Key Distribution Problem

Now imagine a different system. Sandhya installs a secure mailbox outside her home. This mailbox has two keys. A public key, which anyone including Azam can use to lock the mailbox and drop messages inside and a private key, which only Sandhya has and uses to unlock the mailbox and read the messages. In this scenario, Azam does not need to meet Sandhya in person or find a secure channel to share a key. He simply uses her public key to encrypt the message, and only Sandhya can decrypt it with her private key. This is the principle behind asymmetric encryption, also known as public-key encryption. It uses a pair of mathematically linked keys, one public and one private. Anything encrypted with one key can only be decrypted with the other (Diffie & Hellman, 1976; Rivest et al., 1978). Asymmetric encryption solves the key distribution problem, making secure communication possible over open networks like the internet.

Every time you visit a secure website, such as your bank or an email service, your browser uses TLS (Transport Layer Security), which relies on asymmetric encryption to establish a secure session. The website presents its SSL certificate, which contains its public key. Your browser uses this to encrypt a secret "pre-master key." The server decrypts it with its private key, after which both sides can communicate securely (Rescorla, 2001). Payment gateways use public-key cryptography to securely transmit sensitive information such as card details during online transactions, protecting them from interception. In the world of blockchain, asymmetric encryption is also fundamental. Cryptocurrency wallets, for instance, are secured by a private key and a corresponding public key, often hashed to form a wallet address. You can share your public key to receive funds, but only your private key allows you to authorize transactions (Narayanan et al., 2016).

However, the use of asymmetric encryption extends far beyond blockchain. It underpins many of the secure digital experiences we rely on daily, from browsing the internet to making online payments.

Balancing Speed and Security

Symmetric encryption is significantly faster than asymmetric encryption, making it ideal for encrypting large amounts of data efficiently. Asymmetric encryption, while slower due to complex mathematical operations, provides the crucial benefit of secure key exchange. In practice, most secure systems, including your web browser during an HTTPS connection, combine both methods. Asymmetric encryption is used to safely exchange a fresh symmetric key. After that, the symmetric key encrypts the ongoing communication quickly and securely.

Cryptographic Hash Functions (SHA-256 and Immutability)

Let’s continue with the story of Sandhya and Azam to understand another critical building block of digital security: hash functions. Earlier, we saw how they used encryption to keep their messages private. But encryption alone does not reveal if a message or file has been secretly altered. That is where hash functions come in (Stallings, 2017). A hash function is a one-way mathematical process that transforms any input, no matter how large or small, into a fixed-length output called a hash or digest. Even a tiny change to the input produces a completely different hash, making tampering immediately detectable. For example, the widely used SHA-256 algorithm produces a 256-bit hash (NIST, 2015).

Imagine Sandhya keeps a box at home filled with valuable items, arranged in a very specific order. Every time Azam visits, he quickly glances at the arrangement and makes a note of it. This arrangement acts like a fingerprint of the box's contents. If someone secretly opens the box and moves even one item, Azam would immediately notice the change. Similarly, when Sandhya sends a message or file to Azam, she can also share its hash. Azam can run the same hash function on the received file. If the two hashes match, he knows the file is exactly as Sandhya sent it and has not been tampered with (Menezes et al., 1996).

Why Hash Functions Matter?

Hash functions play a crucial role in verifying data integrity across many digital systems. When you download software, the provider often publishes the file's hash. You can compute the hash of your downloaded file and compare it to the published one. If they match, the file is authentic and unaltered. Beyond protecting individual files, hash functions are essential to securing entire blockchain networks. In a blockchain, every block contains its own hash and the hash of the previous block.
This links the blocks together into a continuous, interdependent chain (Narayanan et al., 2016). If someone tries to change the data in one block, its hash also changes, breaking the link to the next block. To successfully alter the blockchain, an attacker would need to recalculate the hashes of that block and all following blocks. This is computationally unfeasible, making unauthorized changes practically impossible. Popular blockchains like Bitcoin and Ethereum rely on hash functions such as SHA-256 and Keccak-256 to secure their networks, detect tampering, and maintain the immutability that is essential for decentralized, trustless systems (Narayanan et al., 2016; Buterin, 2014).

In short, hash functions act like the unchangeable fingerprints of data, allowing individuals like Sandhya and Azam, or entire blockchain communities, to quickly check whether information remains untouched and trustworthy.

Digital Signatures and Message Authenticity

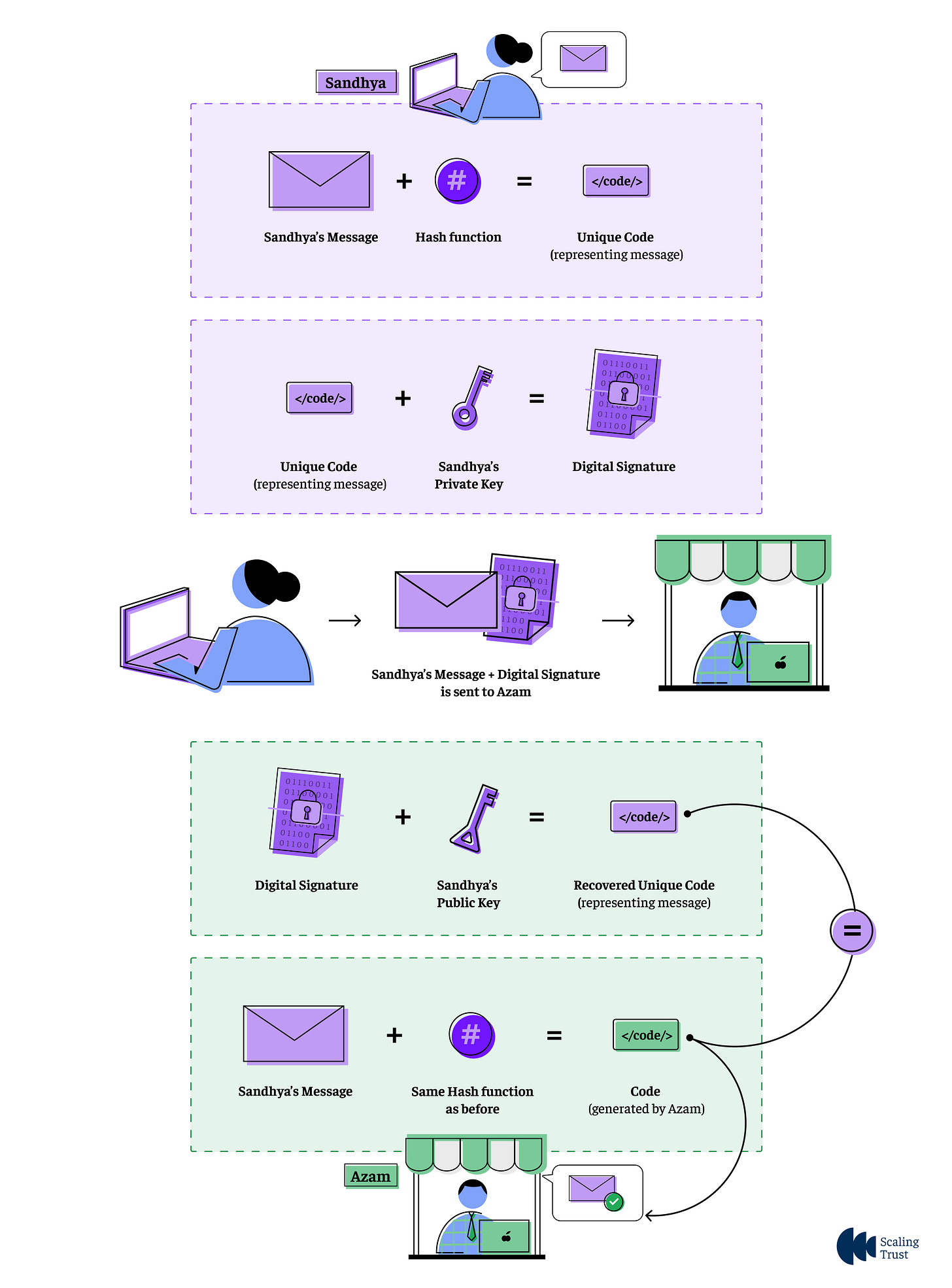
In addition to using encryption and hash functions, Sandhya and Azam rely on another important cryptographic tool to ensure their messages are authentic and tamper-proof. This tool is called a digital signature. Just like a handwritten signature or a wax seal proves who sent a letter, a digital signature proves who created a digital message and whether it has been altered along the way. Digital signatures are based on asymmetric cryptography, where a private key is used to create the signature and a corresponding public key is used to verify it. This mechanism allows Sandhya and Azam to confirm both the identity of the sender and the integrity of the message without relying on a third party (Narayanan et al., 2016).

How It Works?

Imagine Sandhya wants to send an important message to Azam. First, she applies a hash function to the message, creating a short, unique code that represents its contents. She then uses her private key to encrypt this code, generating her digital signature. When Azam receives the message along with Sandhya's digital signature, he uses her public key to decrypt the signature and recover the code that Sandhya originally generated. His software then applies the same hash function to the message he received. If the two codes match, it proves two things:

1. The message was signed using Sandhya's private key, confirming her identity

2. The message was not altered during transmission. Even the slightest change to the message would cause the hashes to differ, invalidating the signature

When you download software or install updates, your device checks the digital signature to ensure the files come from a trusted publisher and have not been tampered with. This process helps protect users from malware and unauthorized changes. Operating systems like Windows, macOS, and mobile platforms rely on this mechanism to maintain software integrity. Platforms like DocuSign, eSign (India’s Aadhaar-enabled signing), and the EU’s eIDAS framework use digital signatures to legally authenticate documents. These signatures provide the same legal validity as handwritten signatures, enabling secure and verifiable digital agreements. =In blockchain and Web3 environments, digital signatures are essential for proving ownership and authorizing actions without the need for central intermediaries. For example, when Sandhya sends a cryptocurrency transaction, her private key digitally signs the transaction data. The blockchain network uses her public key to verify the signature and confirm that the transaction is legitimate. This system secures everything from digital payments and smart contracts to decentralized identity solutions such as "login with Ethereum" (Narayanan et al., 2016).

In short, digital signatures allow Sandhya and Azam, as well as anyone participating in modern digital systems, to communicate, transact, and verify information securely. Whether it is signing a legal contract, downloading software, or interacting with a blockchain, digital signatures ensure that messages and transactions are authentic, unaltered, and verifiable by anyone.

Zero-Knowledge Proofs (Proof without Revealing Data)

So far, Sandhya and Azam have learned how to protect the privacy, integrity, and authenticity of their communications. But what if Sandhya needs to prove to Azam that she knows a secret without revealing the secret itself? As strange as that sounds, cryptography makes this possible through Zero-Knowledge Proofs (ZKPs), a clever protocol that allows one party, known as the prover, to convince another party, the verifier, that a statement is true without revealing any additional information beyond the fact that it is true (Goldwasser, Micali, & Rackoff, 1989).

Imagine Sandhya tells Azam she knows the secret code to unlock a secure room. Naturally, Azam wants proof, but Sandhya does not want to share the code itself. Instead, she steps inside, the door locks behind her, and moments later she opens it from the inside. Azam never learns the code, but he is convinced that Sandhya knows it. This is exactly what zero-knowledge proofs enable in the digital world. They make it possible to prove knowledge or facts without exposing private details.

In blockchain and digital systems, ZKPs are already being used to enhance privacy, scalability, and identity protection. For example, they allow transaction details such as the amount being sent or the identity of participants to remain hidden while still proving to the network that the transaction is valid. Technologies like zk-Rollups help blockchains such as Ethereum process far more transactions efficiently without compromising security (Buterin, 2018). Similarly, ZKPs allow individuals to prove facts about themselves, such as being over 18 years old or owning a specific digital token, without revealing sensitive personal information. A recent example of this concept being applied outside of blockchain comes from India, where age-token solutions based on zero-knowledge principles are being proposed to enable age verification for online platforms without compromising user privacy (Matthan, 2025). This could allow content restrictions to be precisely targeted at minors, while adults retain full access to lawful content.

In short, zero-knowledge proofs are a powerful tool in the modern cryptographic toolkit. They allow people like Sandhya and Azam to protect their privacy while still meeting the requirements of decentralized systems. As blockchain and Web3 technologies continue to evolve, tools like ZKPs will be essential for balancing privacy and transparency.

So, How Does Cryptography Build Digital Trust?

Cryptography creates trust through code, not a central authority. It enables secure, open networks where anyone can independently verify transactions, data integrity, and identity without relying on intermediaries. From securing Bitcoin and Ethereum to powering private digital payments, smart contracts, and tools like zero-knowledge proofs that protect privacy while proving facts, these core techniques are what make decentralized systems work. As we move further into the era of digital assets, Web3, and privacy-first infrastructure like age-token solutions, understanding these fundamentals is essential to appreciating how cryptography quietly builds digital trust behind every secure transaction.

References

Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., & Virza, M. (2014). Zerocash: Decentralized anonymous payments from Bitcoin. IEEE Symposium on Security and Privacy, 459–474. https://doi.org/10.1109/SP.2014.36

Buterin, V. (2014). A next-generation smart contract and decentralized application platform. Ethereum Foundation. https://ethereum.org/en/whitepaper/

Buterin, V. (2018). Plasma and zk-Rollups: Scaling Ethereum. Ethereum Foundation. https://ethereum.org/en/developers/docs/scaling/zk-rollups/

Daemen, J., & Rijmen, V. (2002). The design of Rijndael: AES—The advanced encryption standard. Springer.

Diffie, W., & Hellman, M. (1976). New directions in cryptography. IEEE Transactions on Information Theory, 22(6), 644–654. https://doi.org/10.1109/TIT.1976.1055638

Goldwasser, S., Micali, S., & Rackoff, C. (1989). The knowledge complexity of interactive proof systems. SIAM Journal on Computing, 18(1), 186–208. https://doi.org/10.1137/0218012

Matthan, R. (2025). Moderating with Tokens. Ex Machina. https://paragraph.com/@exmachina/moderating-with-tokens

Menezes, A. J., van Oorschot, P. C., & Vanstone, S. A. (1996). Handbook of applied cryptography. CRC Press.

National Bureau of Standards. (1977). Data Encryption Standard (DES) (FIPS PUB 46). U.S. Department of Commerce. https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.46.pdf

National Institute of Standards and Technology. (2013). Recommendation for key management—Part 1: General (NIST Special Publication 800-57 Part 1, Rev. 4). https://doi.org/10.6028/NIST.SP.800-57pt1r4

National Institute of Standards and Technology. (2015). Secure Hash Standard (SHS) (FIPS PUB 180-4). https://doi.org/10.6028/NIST.FIPS.180-4

Narayanan, A., Bonneau, J., Felten, E., Miller, A., & Goldfeder, S. (2016). Bitcoin and cryptocurrency technologies: A comprehensive introduction. Princeton University Press.

Rescorla, E. (2001). SSL and TLS: Designing and building secure systems. Addison-Wesley.

Rivest, R. L., Shamir, A., & Adleman, L. (1978). A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2), 120–126. https://doi.org/10.1145/359340.359342

Stallings, W. (2017). Cryptography and network security: Principles and practice (7th ed.). Pearson.

Zimmermann, P. (1995). The official PGP user's guide. MIT Press.